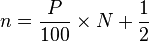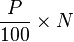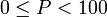85th Percentile Speed Question

[Kram]

Percentile definition: http://en.wikipedia.org/wiki/Percentile



The 25th percentile is also known as the first quartile (Q1), the 50th percentile as the median or second quartile (Q2)…



Median definition: http://en.wikipedia.org/wiki/Median



In statistics and probability theory, median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to highest value and picking the middle one. If there is an even number of observations, then there is no single middle value; the median is then usually defined to be the mean of the two middle values.[1][2]



This is one reason why I do not believe that the 85th percentile speed is always the 85th car’s speed if there is a sample of 100 cars unless I interpreted this incorrectly. If it is true that the 85th car’s speed is the 85th percentile speed then by that definition the 50th car’s speed would then be considered as the 50th percentile speed which is also called the median. However, by the definition of median if there is an even number of observations then the median is then usually defined to be the mean of the two middle values. If you have 100 cars and the speed of the 50th is 45mph and the 51st car is 47mph then the median would be 46mph which would not equal the 50th which is 45mph.



In my understanding the percentile ranges from 0.00 to 1.00 which is 101 values. If 1 to 100 (100 total values) is entered in Excel and the percentile(range:0.50) and percentile(range:0.85) is used the results would be 50.50 and 85.15 respectively. 50.50 will easily make sense because it’s the average of the 50th and 51st values which is also the median. However, if 0 to 100 (101 values representing each percentile) is entered in Excel and the percentile(range:0.50) and percentile(range:0.85) is used then the results would be 50 and 85 respectively. The 85th percentile speed will not be equal to the 85th car; the 85.16th(85/101) or 84th car will more likely be the 85th percentile speed. This brings back to the initial question why the answer would be C.43 instead of D.45; the 84th car is within the range 40-44.

 

[IlPadrino]

Kram,

I agree with your definition and that same Wikipedia page says:

rounding the result to the nearest integer, and then taking the value that corresponds to that rank. (Note that the rounded value of n is just the least integer which exceeds

.)

Of course, this will *increase* the speed of the 85th percentile speed. And in our subject, we agreed it was "at or below", so I think that cancels out the rounding.

You lost me on

The 85th percentile speed will not be equal to the 85th car; the 85.16th(85/101) or 84th car will more likely be the 85th percentile speed. This brings back to the initial question why the answer would be C.43 instead of D.45; the 84th car is within the range 40-44.

You are saying the 85th percentile speed is something faster than the 85th fastest vehicle, yes?

 

[Kram]

You lost me on

The 85th percentile speed will not be equal to the 85th car; the 85.16th(85/101) or 84th car will more likely be the 85th percentile speed. This brings back to the initial question why the answer would be C.43 instead of D.45; the 84th car is within the range 40-44.

You are saying the 85th percentile speed is something faster than the 85th fastest vehicle, yes?

I must have typed it wrong, that 85.16th should have been 84.16th which is the same as 85/101. I am saying that the 85th percentile speed out of 100 sample vehicles is less than the speed of the 85th car. In order for the 85th car to be the 85th percentile, there should be 101 sample cars because the percentile ranges from 0% to 100% which has 101 values. The median which is also the 50th percentile will only be true if the percentile range is based from 0% to 100% because it has an odd number of samples and 50 is the midpoint.

 

[IlPadrino]

With 100 observations, the percentiles (1% to 100%) range from the 1st observation (1%) to the 100th observation (100%)... remember, "at or below". I don't think there's such a thing as the 0th percentile.

 

[ptatohed]

(1) No sir. Please see my post #32 (and jaa's #17). Look at the cumulative column. The cumulative frequency %'s for this problem's speed intervals is 2, 13, 31, 60, 84, 97 and 100%. Since 85% falls between the cumulative 84% and the 97%, interpolation is required to determine the 85th percentile speed.

I wasn't clear... I was talking about the measured speeds, not the binned speeds. So this difference leads us to:

(2) This would be true of there were no recorded speed intervals (bins). If 100 unique speeds were recorded and placed in order then, yes, the 85th fastest speed would be the 85th percentile speed. But per this problem and per many agency's method, the cars passing are counted in a speed interval range (20-24, 25-29 ....... 50-54) . Once speed intervals are used (such as in this problem) and the 85th fastest car falls in one of these intervals, then interpolation is required to solve for the 85th percentile speed. Does that make sense?

I think we're getting somewhere! (1)

Regardless of how speeds are recorded (as measured or binned), they are surely measured in mph. Putting the speeds in bins (whatever their size) only has the effect of losing some (important!) information but the underlying measurement remains unchanged. In this problem of ours, the 85th fastest vehicle is very clearly in the 45-49 bin. So why should any decision on how to create bins (the bigger, the worse for losing information) affect this absolute truth: the 85th fastest vehicle is, without question, traveling between 45 and 49 mph. (2)

To specifically address your last sentence, it makes perfect sense to me: once you know which bin the 85th fastest car falls in, you need to interpolate to solve for the 85th percentile speed. Because there are enough data points, I think it's even fine to linearly interpolate even though the distribution of speeds is best assumed to be normal. (3)

(1)

(2) Yes, you could argue that information is lost. But per the accepted method that many (most?) agencies (and the problem at hand) use to calc the 85th percentile speed, speed intervals (bins) are used during recording/observation and once they are used at the observation stage the, say, 47.8 mph is "lost" and is now placed in the 45-49 bin. Once this is done, the speed is now a 47 mph. Period. That's why the answer to this problem is C (I actually think the answer is closer to 42mph than 43mph but I guess the closest answer is still C). You have 24 cars traveling at an average of 42mph adding up to a cumulative % of 84 (just shy of the 85% we are looking for). You have 13 cars traveling at 47 adding up to a cumulative 97%. The 85% we are looking for is so much closer to the 84% so we know the 85% speed is also going to be closer to the 84% speed (42mph). So, without any additional calcs we can see that the 85% speed will be a little above 42mph but much closer to 42 than 47. Thus, answer C. I hope I am clear. It's easy to think the answer but hard to type it.

(3) I think you lost me. Do you see why the answer is C? I'll try to explain more clearly if not.

 

[IlPadrino]

ptatohed,

There are 100 vehicles for which their speed was recorded. In what bin was the 85th fastest vehicle?

IlPadrino-

 

[Kram]

With 100 observations, the percentiles (1% to 100%) range from the 1st observation (1%) to the 100th observation (100%)... remember, "at or below". I don't think there's such a thing as the 0th percentile.

I agree with your definition and that same Wikipedia page says:

rounding the result to the nearest integer, and then taking the value that corresponds to that rank. (Note that the rounded value of n is just the least integer which exceeds

.)

The first part of the equation quoted from Wikipedia is the following:

One definition of percentile, often given in texts, is that the P-th percentile (

) of N ordered values (arranged from least to greatest) is obtained by first calculating the (ordinal) rank

which suggests that the percentile is from 0% to 99% and includes 0%. After looking at this equation again, I am wrong that there should be 101 values which is from 0% to 100%. The values range from 0% to 99%; if each of the 100 speeds is compared to the percentiles the following would happen: The speed of the 1st vehicle would be 0% because it is not faster than any other vehicle. 2nd vehicle to the 1st percentile until the 85th vehicle which would then be the 84th percentile.

 

[Kram]

I guess since there are different ways of calculating percentiles that give different results, then it will be hard to agree on the same answer; however the 85th fastest car in a sample size of 100 is not necessarily the 85th percentile in my opinion. If there are 100 numbers from 1 to 100 and the following equation is used the 85th percentile would be 85.5;

however if the percentile function of Excel 2003 is used, 84.15 would be the 85th percentile. Assigning each number to the percentile (1 to 0%, 85 to 84%, 100 to 99%) results in the 84 being the 85th percentile.

 

[Kram]

I guess since there are different ways of calculating percentiles that give different results, then it will be hard to agree on the same answer; however the 85th fastest car in a sample size of 100 is not necessarily the 85th percentile in my opinion. If there are 100 numbers from 1 to 100 and the following equation is used the 85th percentile would be 85.5;

however if the percentile function of Excel 2003 is used, 84.15 would be the 85th percentile. Assigning each number to the percentile (1 to 0%, 85 to 84%, 100 to 99%) results in the 84 being the 85th percentile.

Is there a way to edit a post if you make a mistake?

84.15 should be 85.15 and 84 being the 85th should be 86 being the 85th.

 

[IlPadrino]

Is there a way to edit a post if you make a mistake?

84.15 should be 85.15 and 84 being the 85th should be 86 being the 85th.

So how does this change your answer?

 

[ptatohed]

ptatohed,

There are 100 vehicles for which their speed was recorded. In what bin was the 85th fastest vehicle?

IlPadrino-

Il, trust me, I get your point. Yes, the 85th vehicle was in the 45-49 mph speed interval. But the question is not asking "what was the speed of the 85th vehicle?". The question is "what is the 85th percentile speed?". This needs to be calculated. The calculations are previously included in this thread so I don't want to go through them again.

Again, if there were 100 recorded individual speeds, the speed of the 85th fastest car would be the answer (of course, we have no idea what this is in this problem). But, once speed intervals/bins are used in the data collection as they are here and we now have so many cars traveling at 42mph and so many cars traveling at 47, and the 85th percentile speed is somewhere in between, we must use the correct linear interpretation calculations to derive the 85th % speed (calcs previously posted). The best answer is C.

 

[IlPadrino]

Il, trust me, I get your point. Yes, the 85th vehicle was in the 45-49 mph speed interval. But the question is not asking "what was the speed of the 85th vehicle?". The question is "what is the 85th percentile speed?". This needs to be calculated.

OK, so here's a fundamental difference we have. The more I think of it, the better and better this problem is looking as a great problem for the PE exam. Equations should never be blindly followed and especially not when you know they violate the underlying principles. Much earlier in this thread I wrote about the "plug and chug" mentality.

Again, if there were 100 recorded individual speeds, the speed of the 85th fastest car would be the answer (of course, we have no idea what this is in this problem).

And another big disagreement here: of course we have an idea what speed each and every car is travelling because we assume they are normally distributed. 100 samples are surely in the realm of the large numbers.

And let me ask you to do this final thing... putting away all previous discussion in this thread: Go back to the fundamentals of 85th percentile speeds (I gave this http://onlinemanuals.txdot.gov/txdotmanuals/szn/determining_the_85th_percentile_speed.htm but there are surely other sources). And ask yourself this: can binning speeds change the underlying principles of 85th percentile speeds? That is, can the throwing away of information (exact MPH speed) in favor of the convenience for collecting tick marks in a bin on a form, change the underlying process that drives the use of 85th percentile speeds?

Here's what I'm understanding you to say: You agree the 85th fastest vehicle is the definition of the 85th percentile speed. You agree the 85th fastest vehicle is in the 45-49 bin. You want to use an equation that assumes all speeds in a bin are actually at the mean of the bin, even though you know this is not representative of reality. You come up with an answer that you know does not reflect reality. All in favor of following an FDOT recommended process.

Still, I appreciate the discussion especially since we've kept it civil of late! I find this problem fascinating... not sure exactly why.

 

[sac_engineer]

Still, I appreciate the discussion especially since we've kept it civil of late! I find this problem fascinating... not sure exactly why.

I think the rest of us find it fascinating that we're flogging this horse of a question to no end.

It's time to call it a day on this one. The method of calculating the 85th percentile is really a no-brainer and doesn't merit an academic exercise.

 

[IlPadrino]

It's time to call it a day on this one. The method of calculating the 85th percentile is really a no-brainer and doesn't merit an academic exercise.

Keep telling yourself that...

 

[ptatohed]

Il, trust me, I get your point. Yes, the 85th vehicle was in the 45-49 mph speed interval. But the question is not asking "what was the speed of the 85th vehicle?". The question is "what is the 85th percentile speed?". This needs to be calculated.

OK, so here's a fundamental difference we have. The more I think of it, the better and better this problem is looking as a great problem for the PE exam. Equations should never be blindly followed and especially not when you know they violate the underlying principles. Much earlier in this thread I wrote about the "plug and chug" mentality. (1)

Again, if there were 100 recorded individual speeds, the speed of the 85th fastest car would be the answer (of course, we have no idea what this is in this problem).

And another big disagreement here: of course we have an idea what speed each and every car is travelling because we assume they are normally distributed. 100 samples are surely in the realm of the large numbers. (2)

And let me ask you to do this final thing... putting away all previous discussion in this thread: Go back to the fundamentals of 85th percentile speeds (I gave this http://onlinemanuals...ntile_speed.htm but there are surely other sources). And ask yourself this: can binning speeds change the underlying principles of 85th percentile speeds? That is, can the throwing away of information (exact MPH speed) in favor of the convenience for collecting tick marks in a bin on a form, change the underlying process that drives the use of 85th percentile speeds?

Here's what I'm understanding you to say: You agree the 85th fastest vehicle is the definition of the 85th percentile speed. You agree the 85th fastest vehicle is in the 45-49 bin. You want to use an equation that assumes all speeds in a bin are actually at the mean of the bin, even though you know this is not representative of reality. You come up with an answer that you know does not reflect reality. All in favor of following an FDOT recommended process. (3)

Still, I appreciate the discussion especially since we've kept it civil of late! I find this problem fascinating... not sure exactly why.

(1) It appears that you are continuing to look at this problem from a mathematical point of view instead of an engineering point of view. I do very much disagree with your lack of appreciation for pre-established engineering formulas/equations. They are there for a reason! They have been established and agreed upon by engineers before us. Who are we to disregard industry standards and use our own? Why reinvent the wheel? There is an established and agreed upon procedure for determining the 85th percentile speed from collected data. Period. You don't need to agree with it or even like it. But it is the correct way of solving this problem. And it is the answer to this problem and to the original poster's question. I'm actually surprised you think this is such a good problem for the PE exam given that the correct solution is derived from the previously shown method leading to answer C. With all due respect, you'd get this problem wrong if you answered D on the exam. Do you not agree with that?

(2) You are right, we do disagree here. I think that once the exact speed is thrown out in exchange for speed interval tick marks during the data collection, we now no longer know the exact speed each of the cars within an interval was traveling.

(3) Yes, you summed up my answer correctly. I see absolutely no problem with using an industry accepted method to calculate the 85th % speed even if it does not reflect reality as you say it. The same way I'd order 18" pipe even if my calculations showed a 16.2" diameter was needed given my Q (because I know that they don't make 17" pipe). If I calculated a design speed of 54, I'd post 50, not 55. If I was designing curb and gutter on street plans for the City of Anyville, I'd sure as heck use their City Standard Plan for C&G (even though I may personally prefer Std 120-2 of the SPFPWC), if I was calculating the Q coming off of a proposed developed site, I might use a coefficient of runoff a little higher than "reality", to be conservative. Etc. etc.

I hope you get my point. Again, with all due respect, the answer to the original question is C and the previous calculations are correct. That answers the question asked by the original poster.

I'm not really interested in going back and forth any longer about how the answer "should be" this or that. The correct answer is C. If you have questions about how C is derived, I'd be happy to answer. But if you continue to simply repeat yourself that the answer "should be" D, then there isn't much more I can say. Thanks.

 

[IlPadrino]

OK... I tap!

I could respond to most of your post pointing out the apples-to-orange comparison of rounding, pre-established formulas aren't the issue, speed distribution (of course it's normal!), etc... but it will fall on deaf ears (blind eyes?). And referring to local code is silly given we're talking about a national exam.

I've given you a TXDOT procedure for calculating 85th percentile that says "EXAMPLE: Figure 3-2 shows that 125 cars were counted in the northbound direction. So 85 percent would be 106 (125 x 0.85 = 106). Thus, the 106th car (counting up from the bottom) represents the 85th percentile speed." If you want to pretend that an FDOT procedure trumps every other state as well as the underlying SCIENCE behind 85th precentile speeds, have at.

I don't really care if you're giving me all due respect. But, please, respect the science!

One more question, if you please: Would you stake the life of your first-born that the correct answer on an actual NCEES exam would be C? Do you know how exam questions are developed? Oops, that was two question!

You're welcome.

 

[ptatohed]

Well, I do strongly feel that the answer is C. Not so sure I'd bet my Kevin on it though.

 

[YMZ PE]

It gets easier to bet your firstborn when you have a few backups.

j/k - what a cutie!