85th Percentile Speed Question

[IlPadrino]

I looked a similar problem in Traffic Engineering text book by Roess, Prassas and McShane pg. 210

Could you post the similar problem?

 

[sac_engineer]

I think the confusion lies in the way we are interpreting the numbers. The number of vehicles in the sampled set is equal to 100. We think we need to directly convert those numbers to percentiles since the question provides that apparent convenience; however, when solving the problem, the 85th percentile should not be confused with the 85th vehicle. I agree that in the data provided, the 85th vehicle is in the 45-49 bin, but the question isn't asking for that. The 85th percentile is determined from a linear relationship between the accumulated vehicle count at specific speeds (i.e the average of each bin) and the vehicle count percentile. If the bin data were explicit, then the graph would be a stepped, which cannot be used to determine speeds based on percentiles.

 

[civilized_naah]

Could it be that the open intervals have created all the confusion? After all, speeds don't have to be either 25 or 26, they can be in between. Consider the upper ends of the intervals modified as:

Interval Frequency Cumulative

20-25 2 2

25-30 11 13

30-35 18 31

35-40 29 60

40-45 24 84

45-50 13 97

50-55 3 100

Where each interval such as 20-25 basically means >25 - 30

In that case, wouldn't the 84th cumulative frequency correspond to the end of the interval i.e. 45 mph, and the 85th percentile be expected to be just above 45?

 

[IlPadrino]

when solving the problem, the 85th percentile should not be confused with the 85th vehicle.

Here is where we disagree clearly, and I invite you to find any definition of percentile which supports your belief.

I suggest a definition of: "A percentile is a measure that tells us what percent of the total frequency is at or below that measure. A percentile rank is the percentage of measures that fall at or below a given measure."

We could argue whether it is "at or below" or just "below" but that won't make a difference in this case.

There is certainly some interpretation on how to handle percentiles when the sample set is small, but for a sample of 100 it is VERY straightforward.

No one knows how the speeds are distributed in the bin, but can you at least agree that if every car speed was recorded individually (well, they were but for ease of writing the problem it was decided to put them in bins), the 85th percentile would have to be 45 or more?

 

[jaa046]

I looked a similar problem in Traffic Engineering text book by Roess, Prassas and McShane pg. 210

Could you post the similar problem?

for some reason I am not able to upload any more files. If you can give me your email address I would be happy to email it to you.

 

[IlPadrino]

If you'd send to [email protected], I'd appreciate it. Thanks!

 

[IlPadrino]

Major: I think your randomization gives exactly the results expected - thanks for setting it up.

I think sac is trying to copy another problem's solution without really understanding what 85th percentile means. You can't take the mean of a bin and say it's the representative speed of the whole bin's percentile - that's just not how histograms work.

 

[sac_engineer]

jaa046's explanation is correct. Also, we're not talking about histograms, we're talking about percentiles based on average speed.

Also, no one can assume the specific speeds of the vehicles, so for all we know, all 24 cars in the 40-44 mph category could have been travelling at 40 miles per hour. If this is the case (i.e. based on actual speeds), then the 85th percentile is 41 mph.

I'm not disputing the question is ambiguous, I'm just saying that the method of computing the 85 percentile is not the same as just adding the number of cars.

 

[IlPadrino]

Also, we're not talking about histograms, we're talking about percentiles based on average speed.

Yes, we are. A histogram is a way or representing the distribution of data by their frequency.

Also, no one can assume the specific speeds of the vehicles, so for all we know, all 24 cars in the 40-44 mph category could have been travelling at 40 miles per hour. If this is the case (i.e. based on actual speeds), then the 85th percentile is 41 mph.

Not so... even if all 24 vehicles were traveling at 40 mph, the 85th vehicle is still in the 45-49 bin. Really, this is the point of our disagreement, so it would go a long way towards resolution if you could explain why you think the 85th vehicle (after arranging the observed speeds from slowest to fastest) could be anywhere in the 40-44 bin. Would you please address just this difference in our perspectives?

P.S. Major made the assumption that the speeds are randomly distributed, which is as good an assumption as any.

 

[ptatohed]

This is quite the debate! I hope I don't complicate matters even further but I come up with an 85th percentile speed of 42.4 mph, so I guess my answer would be C) 43.

I am trying to attach my calcs, hopefully it will work. Please forgive the poor picture quality - I used the camera on the back of a tablet PC.

What do you guys think?

 

[IlPadrino]

Let me try another angle... if the 85th percentile was in the 40-44 bin, don't you see that the cumulative frequency for that bin would have to be 25? And even still, the 85th percentile would be the highest speed observed in that bin, which is almost assuredly not the mean of the bin.

Really, this comes down to a fundamental understanding of what percentiles means. I wish I could explain it more clearly so sac and others could understand. But so long as they just keep insisting they're right, rather than explaining what the fundamental approach they're taking is, I don't think we'll come to a meeting of the minds.

 

[ptatohed]

Ill, relax dude - this is a friendly discussion.

I see what you guys are saying. And I know for sure the source of our confusion is because the problem statement provides speed intervals instead of 100 exact speeds. But, in the absence of additional data, and not knowing exactly what is going on within each interval, I think it is fair to take the average speed for each interval.

So, in my view (and I could be wrong of course), the 84th speed % of the vehicles was in the range of 40-44 mph, or an average of 42mph in the absence of additional data (in other words, 84% of the observed vehicles were traveling at or below 42mph). Similarly, the 97th speed % was 45-49, or 47mph average. Thus, the speed at which 85% of the observed vehicles are traveling at or below is somewhere between 42mph and 47mph but will be closer to 42 (84th speed %) than 47 (97th speed %).

This, of course, only works if you can make the assumption that, for example, all 18 cars traveling in the 30-34mph interval were traveling at 32mph. Which they probably weren't but, without additional data, I think this is a valid assumption. For all we know, all 18 cars could have been traveling at 30mph, all at 34mph, etc.

I think if it weren't for the speed interval ranges, we'd all be able to easily calculate and agree on an answer. I think it's the interpretation of how to handle the ranges that's wigging us out.

 

[ptatohed]

This, of course, only works if you can make the assumption that, for example, all 18 cars traveling in the 30-34mph interval were traveling at 32mph. Which they probably weren't but, without additional data, I think this is a valid assumption. For all we know, all 18 cars could have been traveling at 30mph, all at 34mph, etc.

But it still isn't correct. Okay, let's do the old excel trick on the assumption that every vehicle in each bin is traveling at the average speed for that bin. In that case the 85th percentile is 47 mph. Do it, go ahead, test your hypothesis.

MH. I totally see what you are saying. And, yes, if you were to simply take the 85th fastest car using my averaging suggestion, that car would be going 47mph. But (and maybe I am looking at this incorrectly) that's not my understanding of how the 85th percentile is established. I was taught to use the formula I showed in my post #32 above.

SD = [ (PD - PMin) / (PMax - PMin) ] (SMax - SMin) + SMin

Where SD = Speed based on your chosen percentile; PD = Your selected percentile (85% in our case); PMin = The cumulative percentage below PD in your distribution table (84% in our case); PMax = The cumulative percentage above PD (97% in our case); SMin = The speed corresponding to PMin (42mph in our case) and SMax = The speed corresponding to PMax (47mph in our case).

You do not simply take the 85th fastest car.

For example, let's say you recorded 25 (out of 100 ) cars at 35mph and 15 cars at 38mph with the 35mph speed falling in the 75% cumulative percent column of your frequency distribution table and the 38mph speed falling in the 88% cumulative percent column on your table. Well, even though the 85th fastest car was going 38mph, that is not the 85th percentile speed. In this example:

SD = [ (85 - 75) / (88 - 75) ] (38 - 35) + 35 = 37.3mph

Applying this formula to the original data provided in post #1 (and using an averaged speed for each interval), SD = 42.4mph

Anyway, that's how I look at it. I hope I made sense.

 

[IlPadrino]

I was taught to use the formula I showed in my post #32 above.

SD = [ (PD - PMin) / (PMax - PMin) ] (SMax - SMin) + SMin

Where SD = Speed based on your chosen percentile; PD = Your selected percentile (85% in our case); PMin = The cumulative percentage below PD in your distribution table (84% in our case); PMax = The cumulative percentage above PD (97% in our case); SMin = The speed corresponding to PMin (42mph in our case) and SMax = The speed corresponding to PMax (47mph in our case).

You do not simply take the 85th fastest car.

OK... I think I understand where your confusion lies. The procedure you've given (linear interpolation) is used to establish the percentile when there is not enough data (i.e. observations) such that one of the speeds is not exactly equal to the percentile of interest. Take a look at http://en.wikipedia.org/wiki/Percentile for an explanation of other methods and note the exception for linear interpolation:

If there is some integer k for which

, then we take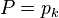

.

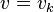
By *definition*, when there are 100 values (as in this problem), the 85th percentile is the 85th largest value when put in rank order. So, yes, you *DO* simply take the 85th fastest car.

 

[IlPadrino]

Ill, relax dude - this is a friendly discussion.

This, of course, only works if you can make the assumption that, for example, all 18 cars traveling in the 30-34mph interval were traveling at 32mph. Which they probably weren't but, without additional data, I think this is a valid assumption. For all we know, all 18 cars could have been traveling at 30mph, all at 34mph, etc.

I'm relaxed... just frustrated that for some (e.g. sac) it's as simple as "I'm undoubtedly right" without enough discussion to come to a resolution. And despite all the posts on this topic, it's still very useful because it will clarify a fundamental understanding of percentiles. You previous post was very helpful in understanding our different approaches.

The central limit theorem does not support your assumption that all observations in the bin are all equal to the average of the bin size (or any other size). It would be reasonable to assume a normal distribution of the entire data set or assume a linear distribution within the bin. It is intuitively *VERY* unlikely that all 24 observations in a bin have the same speed unless they were dependent observations (e.g. all were observed as part of a convoy). If they were independent observations, I'm sure we could calculate the probability.

 

[IlPadrino]

According to DISTRIBUTION OF VEHICLE SPEEDS AND TRAVEL TIMES by DONALD S. BERRY AND DANIEL M. BELMONT of UNIVERSITY OF CALIFORNIA:

"The speeds of vehicles past a point on a highway tend to have a roughly normal distribution except when traffic volume exceeds the practical capacity of the highway."

The data bins certainly look normally distributed to me.

 

[sac_engineer]

By *definition*, when there are 100 values (as in this problem), the 85th percentile is the 85th largest value when put in rank order. So, yes, you *DO* simply take the 85th fastest car.

This is incorrect. If the vehicle counts were doubled (i.e. total of 200 cars in the sample set), you would still think the 85 percentile speed is 45 mph because of your "bin" theory. This is why the vehicle count versus percentile must be mutually exclusive.

Assuming normal/linear distribution within each bin is unrealistic and will not acheive anything closer to reality.

Post #32 is the clear winner in this debate and would get the correct answer in the exam.... which is what it's all about, right?

 

[sac_engineer]

According to DISTRIBUTION OF VEHICLE SPEEDS AND TRAVEL TIMES by DONALD S. BERRY AND DANIEL M. BELMONT of UNIVERSITY OF CALIFORNIA:

"The speeds of vehicles past a point on a highway tend to have a roughly normal distribution except when traffic volume exceeds the practical capacity of the highway."

The data bins certainly look normally distributed to me.

Now you're just being contrary. Your bin theory does not comply to a normal distribution graph; it would a stepped (layer cake) graph. If you visualize the data as a bell-curve graph, then you have to assign a single value within each bin, like a trend line. You would then use this line to determine your percentile vs. speed graph (i.e. the area under the bell curve at each interval divided by the total number in the sample set).

As for your suggestion to assume a normal/linear distribution within each bin, your boundary conditions for each bin would be based the output of the previous bin and the input of the next bin. Does this sound like a realistc approach?

 

[sac_engineer]

Sometimes the accepted method isn't exactly correct, but oh well, I concede.

C'mon...Really? Are you going to die on the sword for this one?

If you had to do this calculation for a client ... say in Florida ...and you were required to put your stamp on it, would you really stray from the standard? I didn't think so.

 

[sac_engineer]

I clearly see something isn't right.