Been trying to review moment distribution method: http://en.wikipedia.org/wiki/Moment_distribution_method
For the life of me I can't figure out why there's a 3, a 4, and a 4 added to the numerator of the flexural stiffnes/distribution factors:
The flexural stiffness of members AB, BC and CD are
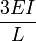 ,
,
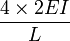 and
and
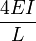 , respectively. Therefore, expressing the results in repeating decimal notation:
, respectively. Therefore, expressing the results in repeating decimal notation:
Can anyone help me with this? thanks.
For the life of me I can't figure out why there's a 3, a 4, and a 4 added to the numerator of the flexural stiffnes/distribution factors:
The flexural stiffness of members AB, BC and CD are
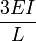
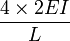
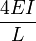
Can anyone help me with this? thanks.






















