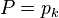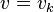I was taught to use the formula I showed in my post #32 above.
SD = [ (PD - PMin) / (PMax - PMin) ] (SMax - SMin) + SMin
Where SD = Speed based on your chosen percentile; PD = Your selected percentile (85% in our case); PMin = The cumulative percentage below PD in your distribution table (84% in our case); PMax = The cumulative percentage above PD (97% in our case); SMin = The speed corresponding to PMin (42mph in our case) and SMax = The speed corresponding to PMax (47mph in our case).
You do not simply take the 85th fastest car.
OK... I think I understand where your confusion lies. The procedure you've given (linear interpolation) is used to establish the percentile when there is not enough data (i.e. observations) such that one of the speeds is not exactly equal to the percentile of interest. Take a look at
http://en.wikipedia....wiki/Percentile for an explanation of other methods and note the exception for linear interpolation:
If there is some integer
k for which
, then we take
.
By *definition*, when there are 100 values (as in this problem), the 85th percentile is the 85th largest value when put in rank order. So, yes, you *DO* simply take the 85th fastest car.