PE Mechanical Machine Design and Materials Practice Problems 510, 533

[jonjjj]

Has anyone been able to solve Problem 510 in the Machine Design and Materials Practice Problems 510 and 533?
 
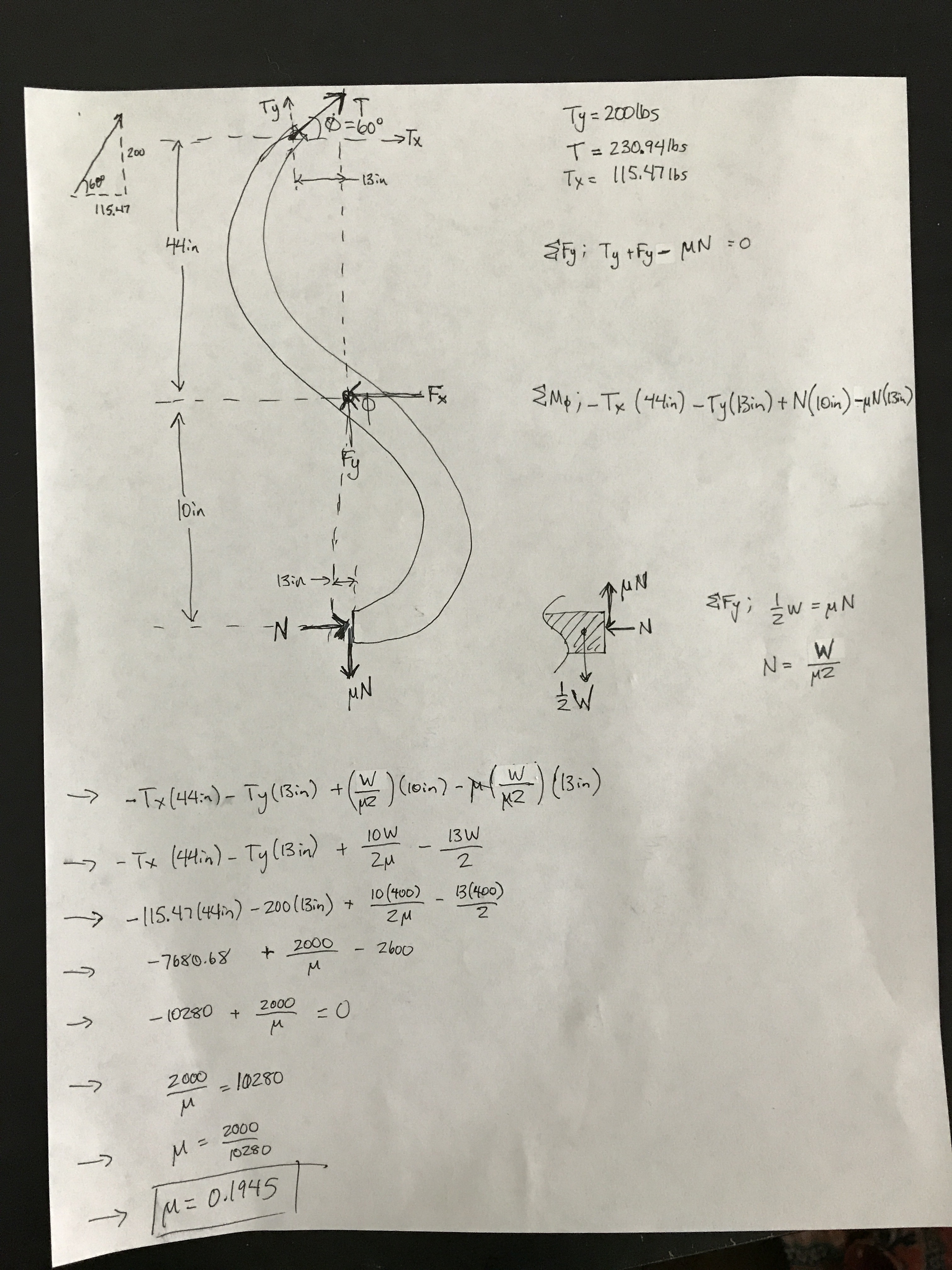
Should the solution to problem 510 take into account the vertical reaction forces caused by the tension of the chain or the weight of the block when determining the normal force between the tongs and the block.  Evaluating one "arm" of the tong and summing the moments around the center pivot, both the vertical and horizontal components of the chain tension contribute moment, as do both the vertical and horizontal reactions at the block/tong interface.  The negative (CW) moments about the center pivot include 200 lbf*13in (vertical component of chain tension) + 115.47lbf*44in (horizontal component of chain tension)  + 200lbf*13in (vertical component of the block/tong interface).  The positive (CCW) moment about the center pivot includes N*10in (Normal force/horizontal component of block/tong interface).
As a result, N = 1028lbf instead of N = 508lbf
The coefficient should be 0.195 instead of 0.394.
 
For Problem 533, then solution uses a yield strength of 73,000 psi, though the problem states 36,500 psi.  Also, the solution uses the Euler critical stress to determine the radius.  Since we're given the load on the rod and a Factor of Safety for buckling, why wouldn't we just solve this using the Euler critical load? 
 
Thank you?

 

[J_MEC]

Hi jonjjj,

I am not sure you are working problem #510 correctly. I solved it and got the same answer as the practice exam. You can view my solution complete with Free Body Diagrams from the dropbox link here: https://www.dropbox.com/s/v5jtfrgcr7ijufb/20170326_191621.jpg?dl=0  Try to compare to your solution and see where you are going wrong.

I have not done problem #533 yet, when I get to it I will let you know what I think.

 

[J_MEC]

Ah, I realized as soon as I posted it, I made a mistake and had a minus sign instead of a + and ended up with the same solution you got. I deleted the link above and have the corrected solution here https://www.dropbox.com/s/2knjv1n5okwgb52/20170326_191621.jpg?dl=0

I agree with you that it looks like a mistake by NCEES.

 

[jonjjj]

Thank you!

 

[jonkytonk]

For 510, try taking a section through the centerline of the entire mechanism then doing a moment balance about the pivot point.

I am also confused by the solution given for 533. I do not agree with their result.

 

[katiejune]

I am also confused on 533 and got 1.57 (C) as my answer.

 

[J_MEC]

Katie, I also got 1.57 (C)

I solved it in a similar manner to what jonjjj describes (Critial Buckling Force is twice the pressure X cylinder area) and used both Euler Curve solution and the parabolic curve solution in Shigley's. The parabolic curve solution yields basically the same result since the slenderness ratio (l over k) is pretty close to the limit for the range that the euler curve solution is accurate.

My solution is at the dropbox link below if you want to compare.

https://www.dropbox.com/s/t2523g1v2n63wuv/20170413_215515.jpg?dl=0

 

[spastic]

Regarding #510, a simple way to think about this problem is to recognize that the vertical component in one chain is equivalent to half the weight of the block. Given the 60deg angle, you can find the horizontal component force at the top and then see that 4.4x this horizontal component is applied at the block.

Regarding #533, The NCEES solution takes the material yield at 73ksi, and then applies the factor of safety to that. The problem states 36.5ksi yield strength, which would be 18.25ksi allowable after the factor of safety is applied. Using these values nets an answer of 1.57in.

 

[J_MEC]

Spastic, where I think you and the NCEES solution are wrong is that you can't say that the horizontal force on the block is 4.4x the horizontal force in the chain. The reason for this is that the friction force (which is a vertical force) produces a moment in the same direction as the vertical component of the chain tension. You might think at a glance the moments they produce cancel each other out since the distance from the point the chain attaches to the surface of the clamp on the block is the same at 13 inches, but they do not because of their directions.

See my free-body diagrams of one of the members of the clamp attached and you should be able to see that uN produces a moment in the same direction as the chain force. You actually don't even need to know the weight of the block to obtain the answer jonjjj and myself got. You can also check out a similar problem on slides 11 and 12 from this slide share.


View attachment 9322

 

[spastic]

Drawing out the FBD, we are in agreement. I wish NCEES would release an errata addressing these inconsistencies. 

 

[turbodudey]

For problem #510, I think the moment due to the vertical forces (chain tension & friction) do cancel out. The friction force acts in the upward direction - opposite to impending motion of the block. This is equal and opposite (same direction, opposite side of the scissor) to the vertical chain tension.

 

[J_MEC]

The friction force is upward on the block (opposite the direction of impending motion) but downward on the clamp (same direction of impending motion). See figure attached from my statics textbook  (Bedford and Fowler). The block in this problem is like the funky shaped object in the figure and the clamp is like the ground.

The moments by the friction force and tension force on the clamp do not cancel each other out since the moments are in the same direction when summed about the center pivot point.

 

[turbodudey]

Yep. You're right. It's the reaction force on the clamp, not the block. So, never mind. Looks like NCEES didn't get this one quite right.