5 replies to this topic

[monkeywinky]

Hi everyone, quick question that hopefully someone can help me understand.

Study material: Spring 2008, Surveying for California Civil Engineering License by Dr. Shahin Mansour

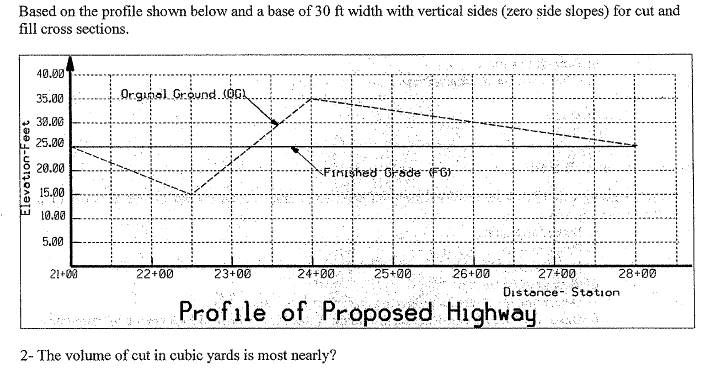
In the practice exam 2, number two, they ask to calculate the cut/fill volumes of a highway profile with 30ft width and vertical sides.

I separated the volume into two triangles and calculated them as such.

The solution, however, says I need to use the pyramid formula, why would that be the appropriate method?



Thanks for the help

[ptatohed]

I believe the prismoidal method (as opposed to the average end area method) is appropriate in this case because you have locations where your areas are zero. I don't have my books with me but I believe the 'aea' method is V=L(A1+A2)/2, right? Well for fill, if you applied this formula between Sta 21+00 to Sta 22+50 (and Sta 22+50 to 23+25), your A1 at Sta 21+00 would be zero. In a case like this, the 'aea' method is not as accurate. Therefore you want to use the 'p' method. I don't remember the 'p' method formula (I think, in addition to A1 and A2, there is a middle area, Am, as well?) but apply the 'p' method four times (twice for fill, twice for cut).
Fill: 21+00 - 22+50 and 22+50 - 23+25. Cut: 23+25 - 24+00 and 24+00 - 28+00. A1 and A2 might be zero in some of the calculations but that's o.k. with the 'p' method. I hope I helped.

[monkeywinky]

Thanks for the reply,

I think the problem I have is that the solution says to use the pyramid formula, Area of base x height / 3.

Let's just say for the cut section, isn't that volume more precisely represented as two wedges?

Volume
STA 23+25 to 24+00
75 x 10 x / 2 x 30 / 27 = 416.7 yd^3

STA 24+00 to 28+00
400 x 10 / 2 x 30 / 27 = 2,222.2 yd^3

=2,639 yd^3 cut

The solution in the book, however, says this

V=(30 x 10)(75+400)/3/27 = 1759.26 yd^3


Just wanted to understand whether this is an error on my part (happens all the time) due to limited understanding or an error in the book (which happens from time to time).

Thanks for taking the time to respond.

I believe the prismoidal method (as opposed to the average end area method) is appropriate in this case because you have locations where your areas are zero. I don't have my books with me but I believe the 'aea' method is V=L(A1+A2)/2, right? Well for fill, if you applied this formula between Sta 21+00 to Sta 22+50 (and Sta 22+50 to 23+25), your A1 at Sta 21+00 would be zero. In a case like this, the 'aea' method is not as accurate. Therefore you want to use the 'p' method. I don't remember the 'p' method formula (I think, in addition to A1 and A2, there is a middle area, Am, as well?) but apply the 'p' method four times (twice for fill, twice for cut).
Fill: 21+00 - 22+50 and 22+50 - 23+25. Cut: 23+25 - 24+00 and 24+00 - 28+00. A1 and A2 might be zero in some of the calculations but that's o.k. with the 'p' method. I hope I helped.

[ptatohed]

Thanks for the reply,

I think the problem I have is that the solution says to use the pyramid formula, Area of base x height / 3.

Let's just say for the cut section, isn't that volume more precisely represented as two wedges?

Volume
STA 23+25 to 24+00
75 x 10 x / 2 x 30 / 27 = 416.7 yd^3

STA 24+00 to 28+00
400 x 10 / 2 x 30 / 27 = 2,222.2 yd^3

=2,639 yd^3 cut

The solution in the book, however, says this

V=(30 x 10)(75+400)/3/27 = 1759.26 yd^3


Just wanted to understand whether this is an error on my part (happens all the time) due to limited understanding or an error in the book (which happens from time to time).

Thanks for taking the time to respond.

I believe the prismoidal method (as opposed to the average end area method) is appropriate in this case because you have locations where your areas are zero. I don't have my books with me but I believe the 'aea' method is V=L(A1+A2)/2, right? Well for fill, if you applied this formula between Sta 21+00 to Sta 22+50 (and Sta 22+50 to 23+25), your A1 at Sta 21+00 would be zero. In a case like this, the 'aea' method is not as accurate. Therefore you want to use the 'p' method. I don't remember the 'p' method formula (I think, in addition to A1 and A2, there is a middle area, Am, as well?) but apply the 'p' method four times (twice for fill, twice for cut).
Fill: 21+00 - 22+50 and 22+50 - 23+25. Cut: 23+25 - 24+00 and 24+00 - 28+00. A1 and A2 might be zero in some of the calculations but that's o.k. with the 'p' method. I hope I helped.

I see what you mean. Sorry, when you first said 'pyramid', I heard 'prismoidal'. In fact, the prismoidal formula would make more sense to me than the pyramid formula. You are right, the end "pieces" would be wedges, not pyramids. Have you tried to solve it just using the average end area method, even though the ends are zero? How about the prismoidal formula method? I bet you'll get really close.

[monkeywinky]

Thanks for the reply,

I think the problem I have is that the solution says to use the pyramid formula, Area of base x height / 3.

Let's just say for the cut section, isn't that volume more precisely represented as two wedges?

Volume
STA 23+25 to 24+00
75 x 10 x / 2 x 30 / 27 = 416.7 yd^3

STA 24+00 to 28+00
400 x 10 / 2 x 30 / 27 = 2,222.2 yd^3

=2,639 yd^3 cut

The solution in the book, however, says this

V=(30 x 10)(75+400)/3/27 = 1759.26 yd^3


Just wanted to understand whether this is an error on my part (happens all the time) due to limited understanding or an error in the book (which happens from time to time).

Thanks for taking the time to respond.

I believe the prismoidal method (as opposed to the average end area method) is appropriate in this case because you have locations where your areas are zero. I don't have my books with me but I believe the 'aea' method is V=L(A1+A2)/2, right? Well for fill, if you applied this formula between Sta 21+00 to Sta 22+50 (and Sta 22+50 to 23+25), your A1 at Sta 21+00 would be zero. In a case like this, the 'aea' method is not as accurate. Therefore you want to use the 'p' method. I don't remember the 'p' method formula (I think, in addition to A1 and A2, there is a middle area, Am, as well?) but apply the 'p' method four times (twice for fill, twice for cut).
Fill: 21+00 - 22+50 and 22+50 - 23+25. Cut: 23+25 - 24+00 and 24+00 - 28+00. A1 and A2 might be zero in some of the calculations but that's o.k. with the 'p' method. I hope I helped.

I see what you mean. Sorry, when you first said 'pyramid', I heard 'prismoidal'. In fact, the prismoidal formula would make more sense to me than the pyramid formula. You are right, the end "pieces" would be wedges, not pyramids. Have you tried to solve it just using the average end area method, even though the ends are zero? How about the prismoidal formula method? I bet you'll get really close.

I agree that the prismoidal would make more sense. On the test, if I run into a problem like such I'll probably use AEA or prismoidal unless otherwise indicated. I haven't found any compelling reason to consider this type of volume as a pyramid. Thanks for the help.

[ptatohed]

So, how close is 1250 CY Fill, 2639 CY Cut (net 1389 CY Cut) to the provided answer?